우리가 데이터를 다룰 때 가장 먼저 마주하는 질문은
“이 수치들의 중심은 어디일까?”, 그리고 “값들이 얼마나 퍼져 있을까?”입니다.
예를 들어, 학급의 시험 점수를 보며 평균이 80점이라면, 우리는 대부분의 학생이 그 언저리에 있다고 추정할 수 있습니다.
하지만 이때 중요한 질문 하나가 추가됩니다. “그 평균 근처에 대부분이 있는가, 아니면 극단적인 값들 때문에 평균만 그렇게 나온 걸까?”
이 두 질문에 답해주는 핵심 도구가 바로 평균(Mean)과 표준편차(Standard Deviation)입니다.
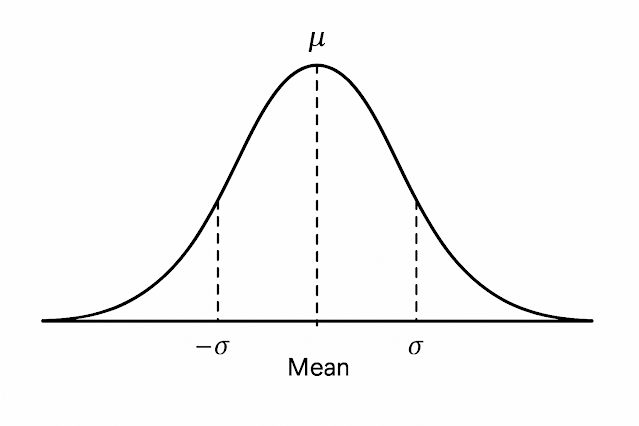
이 두 통계 지표는 기술통계(Descriptive Statistics)의 기초 중의 기초이자, 모든 통계분석의 출발점이라 할 수 있습니다. 평균은 전체 데이터의 중심을 알려주며, 표준편차는 그 중심에서 데이터들이 얼마나 흩어져 있는지를 보여주는 역할을 합니다. 즉, 평균이 '중심 좌표'라면, 표준편차는 그 주변의 '활동 반경'인 셈이지요.
하지만 통계가 처음이신 분들에게는 “그냥 계산기 두드리면 나오는 숫자 아닌가요?”라는 의문도 들 수 있습니다. 하지만 이 숫자들에는 우리의 삶을 설명하고, 예측하며, 결정하는 힘이 담겨 있습니다. 예를 들어 건강검진 결과에서 평균 혈압과 표준편차를 보면 한 집단의 건강 상태를 추정할 수 있고, 마케팅에서는 소비자 만족도 평균과 표준편차를 통해 제품 개선 방향을 잡을 수 있지요.
오늘은 이처럼 중요한 평균과 표준편차를 Jamovi를 통해 직접 구하고 해석하는 방법을 학습하겠습니다. Jamovi는 누구나 무료로 사용할 수 있는 강력한 통계 분석 도구로, 복잡한 명령어 없이 클릭 몇 번으로 원하는 결과를 시각화할 수 있어 초보자에게도 매우 적합합니다.
이제 우리는 통계 분석이라는 거대한 산을 오르기 위한 첫 번째 체력을 기르려 합니다. 평균과 표준편차를 통해 데이터의 얼굴을 읽고, 수치 속에 숨어 있는 의미를 해석하는 법을 하나하나 배워보도록 하겠습니다. Jamovi의 도움으로 더욱 쉽게, 더욱 실용적으로 말이죠.
1. 기술통계란 무엇인가요?
통계학에서 기술통계(Descriptive Statistics)는 ‘있는 데이터를 보기 좋게 정리하는 기술’입니다.
즉, 우리가 수집한 수많은 숫자들을 한눈에 파악할 수 있게 요약해 주는 역할을 합니다. 대표적으로 다음과 같은 지표들이 사용됩니다.

- 중심 경향성 지표: 평균(Mean), 중앙값(Median), 최빈값(Mode)
- 산포도(흩어짐): 범위(Range), 사분위수(IQR), 표준편차(SD), 분산(Variance)
- 분포 특성: 왜도(Skewness), 첨도(Kurtosis)
그중에서도 평균과 표준편차는 기본 중의 기본입니다. 평균은 ‘얼마나 보통인가’를, 표준편차는 ‘얼마나 다른가’를 말해줍니다.
2. 평균(Mean)의 이해 – 중심을 보는 눈
✔ 정의와 수식
평균은 모든 값을 더한 뒤, 데이터 수로 나눈 값입니다. 다음과 같은 수식으로 표현할 수 있습니다:
$$
\bar{X} = \frac{\sum_{i=1}^{n} X_i}{n}
$$
여기서:
- $\bar{X}$: 평균
- $X_i$: 각 데이터 값
- $n$: 데이터의 총 개수
✔ 예시
예를 들어 시험 점수가 70, 80, 90이라면 평균은:
$$
\bar{X} = \frac{70 + 80 + 90}{3} = 80
$$
✔ 해석
평균은 집단의 전반적인 수준을 대표합니다. 그래서 평균 소득, 평균 점수, 평균 속도 등 다양한 분야에서 쓰입니다.
하지만 주의할 점도 있습니다. 평균은 극단값(이상치)에 민감합니다.
예를 들어 한 반의 성적이 대부분 70~80점인데 한 명이 0점을 받는다면 평균은 크게 내려갑니다. 이럴 땐 중앙값이나 표준편차와 함께 보는 것이 안전합니다.
3. 표준편차(Standard Deviation)의 이해 – 퍼짐을 보는 눈
✔ 정의와 수식
표준편차는 각 데이터가 평균에서 얼마나 떨어져 있는지를 수치로 나타낸 것입니다. 다음의 공식을 사용합니다:
$$
SD = \sqrt{\frac{\sum_{i=1}^{n} (X_i - \bar{X})^2}{n}}
$$
위 공식은 모집단 표준편차 공식이며, 표본 표준편차를 구할 경우 $n$이 아니라 $n - 1$로 나눕니다.
✔ 예시
데이터: 60, 70, 80
평균: 70
편차: -10, 0, 10
제곱: 100, 0, 100
합계: 200
표준편차:
$$
SD = \sqrt{\frac{200}{3}} \approx 8.16
$$
✔ 해석
- 표준편차가 작다: 데이터들이 평균 근처에 몰려 있음 (일정함)
- 표준편차가 크다: 데이터가 넓게 퍼져 있음 (다양함)
예를 들어, 두 반의 평균 점수가 같아도 한 반은 60 ~ 90점대, 다른 반은 75 ~ 85점대라면 후자의 표준편차가 작아 성적이 더 고르게 분포되어 있다고 볼 수 있습니다.
4. Jamovi에서 기술통계 실행하기 – 실전 따라하기
Jamovi 실행 및 데이터 불러오기
- Jamovi를 실행합니다.
Data탭에서열기→ ‘.csv’ 또는 ‘.xlsx’ 파일 불러오기.- 원하는 변수(연속형 변수)를 확인합니다. 예:
시험 점수,소득,키,몸무게
Descriptives 모듈 사용법
- 상단 메뉴에서 **
Analyses→Exploration→Descriptives**를 클릭합니다. - 좌측 변수 목록에서 분석할 변수를 오른쪽
Variables로 이동합니다. - 하단의 옵션 메뉴에서 다음 항목을 선택합니다:
- Statistics: Mean, Median, Standard Deviation, Minimum, Maximum
- Plots: Histogram, Boxplot, Density
- Display: Grouped statistics by levels of a factor (선택적으로)
결과 해석 예시

- 평균: 78.3 → 대부분의 점수가 이 근처
- 중앙값: 80.0 → 중앙값이 평균보다 약간 크므로 약간의 왼쪽 왜도 가능성
- 표준편차: 5.2 → 점수들이 대체로 비슷한 범위에 있음
시각화 활용
- 히스토그램(Histogram): 데이터 분포의 형태 확인
- 박스플롯(Boxplot): 이상치 여부와 중앙값 위치 확인
- 밀도그래프(Density): 연속형 데이터의 전체 흐름 시각화
5. Jamovi에서 그룹별 기술통계 구하기
분석 대상이 집단별로 나뉘는 경우 (예: 남녀별, 학년별 등), 다음과 같이 실행합니다.

- Descriptives에서
Split by항목에 범주형 변수를 지정합니다. - 예:
성별을 기준으로소득의 평균과 표준편차를 비교

- 여성의 표준편차가 더 크다면 → 소득 격차가 더 큼
- 평균 차이는 유의성 검정(t-test 등)을 추가로 수행할 수 있습니다.
6. Jamovi 실습을 통한 학습 과제 제안
이해를 높이기 위해 직접 해보는 것이 중요합니다. 다음과 같은 과제를 해보세요:
📌 과제1: 나의 하루 시간 분석
- 데이터 항목: 기상 시간, 공부 시간, 휴식 시간 등
- 분석 항목: 평균, 표준편차, 범위, 히스토그램
📌 과제2: 반 친구들의 키 데이터 분석
- 키 데이터를 수집하고 평균과 표준편차를 구한 후, 그래프 시각화
📌 과제3: 뉴스 데이터 수집 후 기술통계 적용
- 설문조사 결과, 제품 리뷰 평균점수 등 기사 속 데이터를 가져와서 직접 기술통계 분석
숫자 속 이야기를 읽는 힘 – 평균과 표준편차를 통해 본 데이터의 진짜 얼굴
평균과 표준편차. 처음에는 숫자 하나, 수식 하나일 뿐인 것처럼 보였을 수도 있습니다. 하지만 이 두 지표를 제대로 이해하게 되면, 단순한 숫자 그 너머의 ‘데이터가 들려주는 이야기’를 읽을 수 있는 눈을 가지게 됩니다. 이것이 바로 통계를 배우는 진짜 이유이며, Jamovi와 같은 도구를 통해 그 과정을 훨씬 더 직관적으로, 명확하게 실현할 수 있게 된다는 점에서 매우 유의미합니다.
평균은 집단의 중심, 즉 ‘대체로 이렇다’를 말해주는 지표입니다. 한눈에 전체 데이터를 대표할 수 있는 요약값으로서, 교육, 사회조사, 경영, 심리학, 공공정책 등 거의 모든 분야에서 빠짐없이 등장합니다. 그러나 평균은 어디까지나 중심값일 뿐이며, 때로는 극단값에 의해 왜곡될 위험이 있다는 한계를 안고 있습니다.

그래서 표준편차가 반드시 함께 고려되어야 합니다. 표준편차는 숫자들이 평균 근처에 몰려 있는지, 아니면 멀리 흩어져 있는지를 알려줍니다. 이를 통해 “평균만 봐선 알 수 없는, 데이터의 숨은 다양성”을 포착할 수 있게 됩니다. 예를 들어 두 기업의 직원 평균 연봉이 똑같이 5,000만 원이라 해도, 표준편차가 크면 어떤 직원은 3,000만 원, 어떤 직원은 7,000만 원을 받고 있을 수 있다는 의미지요. 반면 표준편차가 작다면 모두가 비슷한 연봉을 받고 있다는 것을 나타냅니다.
Jamovi를 통해 이 두 지표를 실습하면서 우리는 단순한 수학적 계산 이상의 것을 배웠습니다. 복잡한 코드나 수식을 입력하지 않아도 클릭 몇 번으로 평균과 표준편차, 그리고 히스토그램, 박스플롯, 왜도·첨도 같은 지표들까지도 함께 확인할 수 있었고, 그 결과를 직관적인 시각화로 해석해볼 수 있었습니다. Jamovi는 초보자에게도 매우 친절한 통계 분석의 동반자가 되어줍니다.
또한 우리는 기술통계가 단지 ‘숫자 정리’만이 아니라는 것을 알게 되었습니다. 그것은 ‘현상을 요약하고 이해하는 출발점’입니다. 모든 추론, 비교, 예측, 가설검정의 전 단계에 반드시 선행되어야 하며, 이 과정을 정확하게 수행하지 못하면 통계 분석의 신뢰도 자체가 흔들릴 수 있습니다. 다시 말해, 기술통계는 ‘기초’인 동시에 ‘전략’이기도 한 셈입니다.
이제 여러분은 평균이 단지 “합해서 나누는 숫자”가 아니라, 그 자체로 하나의 이야기 구조이며, 표준편차는 그 이야기 속에서 얼마나 다양한 목소리가 섞여 있는지를 알려주는 지표라는 사실을 체감하셨을 것입니다.
다음 학습 안내
Day 13에서는 드디어 본격적인 비교 분석에 들어갑니다. 두 집단의 평균을 비교하는 대표적 통계 기법인 독립표본 t검정(Independent Samples t-Test)에 대해 배울 예정입니다. Jamovi를 활용해 집단 간 차이가 통계적으로 유의미한지를 검정하는 방법, 등분산 가정(Levene's Test), 유의확률(p-value)의 해석법 등을 아주 자세하게 알아볼 거예요.
마무리 미션
다음과 같은 내용을 정리하며 오늘 학습을 복습해보세요:
- Jamovi에서 Descriptives 모듈을 활용해
평균,중앙값,표준편차를 구하고 그래프로 확인해보기 - 뉴스나 보고서에서 기술통계가 사용된 예시를 찾아보고, 그 수치가 어떤 의미인지 분석해보기
- 같은 평균을 가진 서로 다른 데이터셋을 만들어 표준편차를 비교해보기 (예: [70,70,70] vs [50,70,90])
마무리 한마디
숫자는 거짓말을 하지 않지만, 우리가 그 숫자를 해석할 줄 모른다면 마치 아무 말도 하지 않는 것과 같습니다.
평균과 표준편차는 우리가 숫자와 대화를 시작하는 첫 문장이며, 통계라는 언어의 기본 어휘입니다.
오늘 배운 내용을 토대로, 통계를 점점 더 자신 있게 다룰 수 있게 되시기를 진심으로 응원합니다.
'논문 연구 > 논문 통계' 카테고리의 다른 글
| Day 14: 세 집단 이상 평균 차이를 과학적으로 비교하는 방법 – 일원분산분석(ANOVA) 완전 정복 (5) | 2025.08.04 |
|---|---|
| Day 13: 그룹 간 평균 비교 – 독립표본 t검정 (Independent Samples t-Test) (6) | 2025.08.03 |
| Day 11: 교차분석으로 관계를 보다 – 범주형 변수의 연결고리를 찾아서 (4) | 2025.08.02 |
| Day 10: 빈도분석 완전정복 - 명목형·서열형 변수 분석의 모든 것 (1) | 2025.08.02 |
| Day 9: 변수 레이블, 값 레이블, 데이터 정리 - Jamovi에서 데이터 정리를 완벽하게! (4) | 2025.08.02 |

