통계는 관계를 밝혀내는 언어입니다
통계를 배우다 보면, 처음에는 숫자의 집합처럼 느껴지던 데이터가 어느 순간 말없이 많은 이야기를 하고 있다는 것을 느끼게 됩니다.
처음에는 단지 숫자들이 나열되어 있는 것처럼 보이지만, 그 숫자들 사이에는 어떤 규칙성, 경향성, 그리고 때로는 의미 있는 인과관계가 숨어 있습니다.
특히 우리가 흔히 접하는 사회조사나 마케팅 리서치, 여론조사 결과 등을 조금 더 깊이 이해하려면, 단일 변수의 빈도나 평균만으로는 부족합니다. 두 변수 간의 관계, 다시 말해 “이것과 저것은 관련이 있을까?”라는 질문에 대답할 수 있어야 합니다.
이때 필요한 분석 방법이 바로 교차분석(Cross Tabulation Analysis)입니다.
교차분석은 두 개 이상의 범주형 변수 간의 관련성을 탐색하는 데 사용되는 대표적인 통계 기법입니다. 예를 들어, 한 제품에 대한 만족도가 성별에 따라 차이가 있는지를 알고 싶다면, “성별”이라는 변수와 “만족도 수준”이라는 변수 간의 교차분석을 통해 각 범주 간 분포 패턴의 차이를 시각적으로 확인하고, 그 차이가 우연에 의한 것인지, 통계적으로 유의미한 것인지를 판단할 수 있습니다.
많은 분들이 통계를 어려워하는 이유 중 하나는 수식이 복잡하거나, 분석 결과를 어떻게 해석해야 할지 감이 잘 오지 않기 때문입니다. 하지만 교차분석은 데이터를 표로 정리하여 시각적으로 비교할 수 있다는 점에서 직관적이며, 특히 Jamovi 같은 통계 프로그램을 활용하면 버튼 몇 번의 클릭만으로도 결과를 도출할 수 있습니다. 그러므로 교차분석은 통계 입문자에게도 매우 적합한 분석 방법 중 하나입니다.
또한 교차분석은 변수 간의 분포를 나열하는 것에 그치지 않고, 카이제곱 검정(χ² test)이라는 통계적 추론 방법을 통해 두 변수 간의 독립성 여부를 객관적으로 판단할 수 있는 도구로 확장됩니다.
예를 들어, "성별과 직업 만족도 사이에는 통계적으로 유의한 관계가 있다"라고 말할 수 있는 근거를 마련해주는 것이죠. 이러한 분석은 특히 설문조사, 사회학 연구, 심리학 실험, 마케팅 데이터 분석 등에서 자주 활용됩니다.
이번 글에서는 교차분석의 개념부터 시작해서, 실제 Jamovi 프로그램을 활용하여 Crosstabs 모듈을 통해 교차표를 만드는 방법, 기대빈도 확인, 카이제곱 통계량 계산, 그리고 그 결과를 시각화하는 과정까지 모두 익힐 수 있도록 해보겠습니다.
교차분석은 ‘기술통계’에서 ‘추론통계’로 넘어가는 중요한 다리 역할을 하는 분석 도구로, 앞으로 배우게 될 회귀분석이나 요인분석 등과도 긴밀하게 연결되어 있습니다.
교차분석을 제대로 이해하면, “몇 명이 그렇다더라” 수준에서 벗어나 “이러한 경향성은 우연이 아니다”라는 보다 깊이 있는 해석을 할 수 있습니다. 이 분석을 통해 여러분은 숫자의 나열 속에서 패턴을 찾아내고, 해석하며, 의미를 구성하는 힘을 기르게 될 것입니다.
1️⃣ 교차분석이란 무엇인가요?
교차분석(Cross Tabulation Analysis)은 두 개 이상의 범주형 변수 간의 관계를 파악하기 위한 통계 분석 기법입니다. 이 분석은 데이터를 교차표(cross tabulation table)의 형태로 배열하여 변수 간의 상호 분포를 시각적으로 이해할 수 있게 해줍니다.
예를 들어, 다음과 같은 질문을 생각해봅시다.
“남성과 여성은 선호하는 커피 종류에 차이가 있을까?”
이 질문은 성별(남/여)이라는 명목형 변수와 커피 종류(아메리카노/라떼/에스프레소)라는 또 다른 명목형 변수 사이의 관계를 묻고 있습니다. 이 둘을 행(row)과 열(column)에 각각 배치한 뒤, 교차빈도표를 작성하면 성별에 따른 선호 경향을 쉽게 볼 수 있습니다.

2️⃣ 교차표(Crosstab)의 구조 이해하기
다음은 성별과 커피 선호도에 대한 예시 교차표입니다:
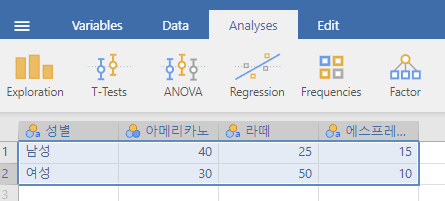
| 아메리카노 | 라떼 | 에스프레소 | 합계 | |
| 남성 | 40 | 25 | 15 | 80 |
| 여성 | 30 | 50 | 10 | 90 |
| 합계 | 70 | 75 | 25 | 170 |
위 표에서는 빈도수만을 볼 수 있지만, 교차분석에서는 이 표를 기반으로 다음과 같은 분석을 진행합니다:
- 행과 열의 비율 계산
- 행 백분율 / 열 백분율 보기
- 두 변수의 독립성 여부 판단(카이제곱 검정)
3️⃣ 카이제곱 검정(χ² test): 독립성 분석의 핵심
카이제곱 검정(Chi-Square Test)은 두 범주형 변수 간의 독립성(independence)을 통계적으로 검정하는 기법입니다. 쉽게 말해, 변수 A와 변수 B가 서로 관련이 있는지를 확인하는 것입니다.
💡 수식
$$
\chi^2 = \sum \frac{(O - E)^2}{E}
$$
- $O$: 관측빈도(Observed frequency)
- $E$: 기대빈도(Expected frequency)
→ $E = \frac{\text{행합} \times \text{열합}}{\text{전체합}}$
✅ 예시
위 표에서 남성이 아메리카노를 선택한 빈도는 40입니다.
기대빈도 $E$는:
$$
E = \frac{80 \times 70}{170} ≈ 32.94
$$
이 값을 사용해 χ² 값을 계산하고, 자유도(df)와 유의수준(보통 0.05)을 기준으로 p-값을 산출하면 두 변수 간 관계가 우연이 아닌지를 판단할 수 있습니다.
4️⃣ Jamovi 실습: 교차분석 직접 해보기
① 데이터 준비
- Jamovi를 열고 [Data] 탭에서 데이터를 입력하거나 엑셀(.xlsx) 파일을 불러옵니다.
- 두 개의 명목형 또는 서열형 변수를 준비합니다. (예: 성별, 커피 선호도)
② 분석 메뉴 선택
- 상단 메뉴에서 "Frequencies" → "Contingency Tables" → "Crosstabs" 클릭
- 변수 중 하나를 Rows, 다른 하나를 Columns로 배치
③ 옵션 설정
- Counts: 기본 교차빈도표
- Row percentages: 행 기준 비율
- Column percentages: 열 기준 비율
- Chi-square test of independence: 독립성 검정
- Expected counts: 기대빈도 표시
④ 결과 해석
- 교차표를 통해 시각적으로 분포 확인
- χ² 검정 결과에서 p-값이 0.05보다 작으면 → 통계적으로 유의미한 관계
- Expected counts와의 차이 확인 → 카이제곱 통계량의 핵심
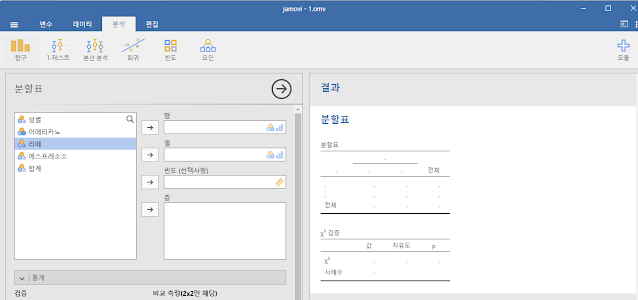
5️⃣ 교차분석의 시각화 – Bar Plot 활용
Jamovi에서는 교차분석의 시각화를 위해 **막대그래프(Bar Plot)**를 생성할 수 있습니다.
- 상단에서 [Exploration] → [Descriptives] → 변수 선택
- [Plots] 항목에서 Bar plot, Stacked bar plot 선택 가능
- 명목형 변수 간 비교 시 시각적으로 차이가 쉽게 드러납니다.
6️⃣ 교차분석이 적합한 경우 vs 그렇지 않은 경우
| 분석 조건 | 교차분석 적합 여부 |
|---|---|
| 두 변수 모두 범주형 (명목 or 서열형) | ✅ 가능 |
| 하나는 범주형, 다른 하나는 연속형(나이 등) | ❌ 적합하지 않음 |
| 두 변수 모두 연속형 | ❌ 상관분석 필요 |
📌 Tip: 변수 유형을 잘못 판단하면, 분석 자체가 왜곡될 수 있습니다.
Day 2에서 배운 변수 유형 정리가 이때 중요한 이유입니다.
Day 2: 변수의 세계로 첫 발! - 명목형, 서열형, 구간형, 비율형 변수 완전정복
“변수요? 그게 뭐예요? 이름이 왜 이리 어렵죠?” 처음 통계를 접하면 가장 먼저 마주치는 단어 중 하나가 바로 변수(variable)입니다.이 단어만 보면 머리가 아픈 분들, 걱정 마세요!오늘은 변수
storymoti.com
7️⃣ 교차분석의 한계와 주의점
- 데이터 수가 너무 적으면 카이제곱 검정이 부적합할 수 있음
- 특히 기대빈도(E)가 5 이하인 셀이 많으면 Fisher's Exact Test를 사용해야 함
- 변수 수가 많아질수록 교차표가 복잡해짐
- 두 변수 이상을 동시에 분석할 땐 로지스틱 회귀 등 고급 분석 도입 고려
- 범주 설정 방식에 따라 결과가 달라질 수 있음
- 예: 연령을 20대/30대/40대로 구분 vs 10살 단위 구분 → 분석 결과 차이
8️⃣ 교차분석의 실생활 활용 예시
| 적용 분야 | 예시 질문 |
|---|---|
| 사회 조사 | 성별에 따라 정치 성향이 다를까? |
| 마케팅 조사 | 연령대에 따라 선호하는 광고 유형은 다를까? |
| 교육 연구 | 학교 유형에 따라 진로 만족도가 달라질까? |
| 보건 통계 | 흡연 여부와 질병 발병률 간에 유의미한 관련이 있을까? |
실제로 많은 논문에서 교차분석은 서론 다음 결과 분석의 시작점으로 자주 등장합니다. 그만큼 기본적이면서도 강력한 도구입니다.
옵션 설명
1. Tests (검정 항목)
χ² (Chi-square)
- 가장 기본적인 독립성 검정입니다. 두 범주형 변수(예: 성별과 커피 종류)가 서로 연관이 있는지를 통계적으로 검정합니다.
- 예를 들어, “성별에 따라 선호 커피가 달라지는가?”라는 질문에, 실제 관측된 빈도와 기대되는 빈도 간 차이를 바탕으로 p값을 산출합니다.
- 이 옵션은 교차분석에서 거의 항상 사용되는 기본 도구이며, 표본 수가 충분할 때 가장 정확한 결과를 제공합니다.
χ² continuity correction
- χ² 검정은 연속형이 아닌 이산형 분포에 가까워서, 특히 2×2 교차표에서 약간의 과대 추정을 할 수 있습니다.
- 이를 보완하기 위해 Yates continuity correction을 적용할 수 있으며, 이는 통계량을 조금 보수적으로 조정하여 p값이 커지는 경향이 있습니다.
- 소표본 2×2 교차표일 때 사용을 고려합니다.
Likelihood ratio
- χ² 검정의 대안으로 우도비(우도검정 통계량)를 활용한 방법입니다.
- 이 역시 변수 간 독립성 여부를 판단하지만, 기대빈도가 낮을 때 조금 더 유연한 결과를 제공합니다.
- 일반적으로 고급 분석에서 비교 목적으로 활용됩니다.
Fisher’s exact test
- 표본 수가 매우 작거나, 어떤 셀의 기대빈도가 5보다 작을 때 사용하는 정확한 검정 방법입니다.
- 특히 교차표 셀의 값이 적을 경우 χ² 검정은 신뢰도가 떨어질 수 있는데, 이때 Fisher's test는 정확한 확률 기반 검정을 수행합니다.
- Jamovi는 셀이 작은 2×2 교차표일 때 자동으로 권장하기도 합니다.
z test for difference in proportions
- 이 검정은 두 비율의 차이를 z 통계량으로 비교합니다.
- 예를 들어 남성 중 60%가 아메리카노를 좋아하고 여성은 30%일 때, 이 차이가 통계적으로 유의한지를 z-검정으로 판단합니다.
- χ² 검정보다 비율의 직접 비교에 초점을 둡니다.

2. Hypothesis (가설 설정)
Group 1 ≠ Group 2
- 기본 설정이며, 두 집단(예: 남성 vs 여성) 간 차이가 존재하는지를 검정합니다.
- 이는 양측 검정(two-tailed test)으로, 어느 쪽이 크거나 작을지 방향을 특정하지 않은 상태에서 차이를 탐색합니다.
Group 1 > Group 2 / Group 1 < Group 2
- 단측 검정(one-tailed test)으로, 특정 방향의 차이가 존재한다고 가정합니다.
- 예: “남성이 여성보다 아메리카노를 더 선호한다”처럼 방향이 명확할 때 사용하지만, 학술적으로는 양측 검정이 일반적입니다.
3. Comparative Measures (비교 지표 – 2×2 전용)
※ 아래 항목들은 2×2 교차표일 때만 활성화됩니다.
Odds ratio (오즈비)
- 사건 발생의 “기회 비율”을 비교합니다. 예: 남성이 여성보다 커피를 마실 가능성이 얼마나 높은가.
- 의료·심리학 분야에서 질병의 유병률 등과 관련하여 자주 사용됩니다.
Log odds ratio
- Odds ratio의 로그값으로, 회귀 분석이나 로지스틱 회귀에서 선형적 해석을 위해 자주 쓰입니다.
Relative risk
- 사건 발생의 “위험 비율”을 비교합니다. 예: 남성이 여성보다 커피를 마실 ‘위험’이 몇 배 높은가.
- 보건통계에서 위험도 비교에 유용한 지표입니다.
Difference in proportions
- 두 집단 간 비율의 직접적인 차이를 수치로 표시합니다.
- 예: 남성 60%, 여성 40% → 차이 = 20%
Confidence intervals
- 위 지표들(오즈비, 비율 차이 등)에 대한 신뢰구간(보통 95%)을 함께 표시합니다.
- 결과의 정확도와 신뢰도를 확인하는 데 유용하며, 해석 시 중요 정보입니다.
4. Nominal / Ordinal Measures
Contingency coefficient
- 명목형 변수 간 연관성의 정도(0~1)를 측정하는 계수입니다.
- χ² 값 기반으로 계산되며, 값이 클수록 관계가 강하다는 뜻입니다.
Phi and Cramer’s V
- 2×2 교차표에는 Phi coefficient, 2×2 이상에는 Cramer’s V를 사용합니다.
- Cramer’s V는 두 변수 간 관계의 강도(0~1)를 정량화하며, 다음과 같이 해석합니다:
- 0.1 이하 → 매우 약함
- 0.1~0.3 → 약한 관계
- 0.3~0.5 → 중간 정도
- 0.5 이상 → 강한 관계
Gamma, Kendall's tau-b, Mantel-Haenszel
- 이 항목들은 서열형 변수 간의 상관관계를 측정합니다.
- 예를 들어, 교육 수준(초졸, 중졸, 고졸)과 만족도(불만족~매우 만족)의 순서 관계 분석에 유용합니다.

5. Counts / Percentages (빈도 및 비율 출력 설정)
Observed counts
- 교차표에 실제 관측된 값(빈도 수)을 표시합니다.
Expected counts
- 변수 간 독립이라고 가정할 때 기대되는 빈도를 계산해 표시합니다.
- χ² 검정에서는 이 기대값과 관측값의 차이를 비교하여 통계량을 계산합니다.
Percentages
- 선택한 기준에 따라 교차표에 백분율 표시를 추가합니다.
- ✅ Row: 각 행 기준 비율 표시 (예: 남성 중 몇 %가 라떼를 선택했는가)
- ⬜ Column: 각 열 기준 비율
- ⬜ Total: 전체 응답 중 해당 셀이 차지하는 비율
6. Post Hoc Tests (잔차 분석)
Unstandardized residuals
- 관측값 – 기대값의 차이를 수치로 나타냅니다.
Pearson residuals
- Pearson 방식으로 정규화한 잔차로, 큰 값은 모델과 기대치의 괴리를 의미합니다.
Standardized residuals
- 표준편차 단위로 정규화된 잔차입니다. 통상적으로 2 이상이면 통계적으로 의미 있는 셀로 간주됩니다.
Adjusted residuals
- 카이제곱 통계량을 조정해 잔차를 더 정교하게 산출합니다.
- 교차표 셀이 많고 해석이 복잡할 때 유용합니다.
📌 Highlight values above: 특정 잔차 값 이상인 셀을 강조해서 표시합니다.
7. Plots (시각화 설정)
Bar Plot
- 교차표 결과를 막대그래프 형태로 시각화합니다. 직관적인 해석이 가능해집니다.
Bar Type
- Side by side: 각 범주를 나란히 막대로 보여줍니다 (그룹 비교에 좋음)
- Stacked: 하나의 막대에 여러 값 누적 (전체 구성 비율 보기)
Y-Axis
- Counts: 빈도 수 기반 막대
- Percentages: 비율 기반 막대
X-Axis
- 막대의 그룹화 기준을 행(Row) 또는 열(Column) 변수로 설정합니다.
요약
| 기능 | 설명 요약 |
| χ² 검정 | 두 변수 간 독립성 판단의 핵심 |
| Cramer's V | 관계 강도 정량화 (0~1) |
| Fisher's test | 표본 수 적을 때 정확한 검정 |
| 기대빈도 표시 | χ² 검정 해석 필수 요소 |
| Row Percent | 그룹 내 구성 비율 해석 |
| Bar Plot | 시각적으로 한눈에 비교 가능 |
관계를 보는 눈을 길러주는 교차분석, 통계의 새로운 시작
통계는 숫자를 계산하는 학문이 아닙니다.
데이터를 통해 세상의 구조와 패턴, 그리고 인간 행동의 법칙성을 탐색하는 지적 도구입니다.
이번 학습에서는 교차분석의 개념부터 실제 분석 과정, 그리고 결과 해석에 이르기까지 전 과정을 체계적으로 살펴보았습니다. 먼저, 교차분석은 두 변수 간의 분포를 교차표(crosstab)라는 형태로 정리함으로써, 변수 간의 관계를 시각적으로 드러내는 데 큰 장점을 갖고 있다는 점을 배웠습니다. 이 교차표를 기반으로 행 또는 열 기준의 백분율을 계산하면, 숫자를 넘어서 경향성이나 비율의 차이를 분석할 수 있습니다.

그리고 이러한 비교에서 한 걸음 더 나아가, 카이제곱 검정(χ² test)을 통해 변수 간 관계가 통계적으로 유의미한지 아닌지를 검정할 수 있었습니다. 이는 분석이 정량적 추론으로 확장된다는 것을 의미합니다. 관측된 빈도와 기대빈도 간 차이를 수학적으로 계산하고, 이를 통해 “관계가 있다 / 없다”는 결론을 내릴 수 있게 된 것이죠.
이처럼 교차분석은 기술통계의 시각화적 측면과 추론통계의 검증적 측면을 동시에 포함한 하이브리드 도구라고 할 수 있습니다.
Jamovi를 통한 실습을 통해 복잡한 수식이나 코딩 없이도, Crosstabs 모듈을 활용하여 교차표 생성, 백분율 계산, 카이제곱 검정 결과 도출까지 일관된 흐름으로 분석할 수 있었을 것입니다. 특히 기대빈도, p값, 유의수준 등의 개념을 Jamovi 인터페이스 안에서 실시간으로 확인하고 해석할 수 있었던 경험은, 실무적 감각을 키우는 데 큰 도움이 되었을 것이라 생각합니다.
물론 교차분석에도 한계는 존재합니다.
기대빈도가 낮은 셀이 많을 경우, 검정 결과의 신뢰도가 떨어질 수 있으며, 두 변수 외의 제3의 변수로 인한 혼동 효과(confounding effect)는 반영하지 못합니다. 따라서 보다 복잡한 현상에 대해서는 다변량 분석(예: 로지스틱 회귀분석, 구조방정식 등)이 필요할 수 있습니다. 그러나 교차분석은 그러한 고급 통계로 나아가기 위한 가장 기초적이면서도 핵심적인 첫걸음이라는 점에서 반드시 확실하게 숙지하고 넘어가야 할 기법입니다.
또한 이번 교차분석 학습을 통해, Day 2에서 배운 변수의 유형 분류(Nominal, Ordinal 등)이 얼마나 중요한지를 실감하셨을 것입니다. 변수를 어떻게 분류하느냐에 따라 적용할 수 있는 통계 방법이 완전히 달라지며, 해석의 방향도 달라집니다. 따라서 앞으로 통계분석을 할 때마다 항상 “내가 분석하려는 변수는 어떤 유형인가?”를 먼저 점검하는 습관을 들이시길 바랍니다.
다음 학습으로 연결하며: 통계에서 비교란 무엇인가?
이제 여러분은 두 개의 범주형 변수 간의 관계를 분석하는 교차분석을 마스터하셨습니다.
다음 단계는 집단 간 차이를 비교하는 방법입니다. 즉, 평균 비교라는 새로운 질문을 던지게 됩니다.
“남성과 여성의 평균 키는 차이가 있을까?”
“이 제품에 대한 만족도가 지역에 따라 다른가?”
“새로운 교육 프로그램을 받은 그룹과 받지 않은 그룹의 성적 평균은 다를까?”
이러한 질문은 교차분석과 달리, 연속형 변수의 평균을 두 집단 또는 그 이상에서 비교하는 것이 핵심입니다. 다음 Day 12에서는 이러한 분석을 수행할 수 있는 방법인 기술통계 분석(Descriptive Statistics)과 t검정(t-test), 분산분석(ANOVA) 등의 기초를 배워가게 될 것입니다.
'논문 연구 > 논문 통계' 카테고리의 다른 글
| Day 13: 그룹 간 평균 비교 – 독립표본 t검정 (Independent Samples t-Test) (6) | 2025.08.03 |
|---|---|
| Day 12: 기술통계 - 평균, 표준편차 구하기 (7) | 2025.08.02 |
| Day 10: 빈도분석 완전정복 - 명목형·서열형 변수 분석의 모든 것 (1) | 2025.08.02 |
| Day 9: 변수 레이블, 값 레이블, 데이터 정리 - Jamovi에서 데이터 정리를 완벽하게! (4) | 2025.08.02 |
| Day 8: Jamovi 기본 화면과 데이터 입력 방법 (0) | 2025.08.02 |

