Day 13: 그룹 간 평균 비교 – 독립표본 t검정 (Independent Samples t-Test)

삶을 그리다 2025. 8. 3. 22:41

“과연 두 집단은 정말 다를까?” – 그 질문에 통계가 답하다

통계를 배운다는 것은 숫자를 계산하는 기술을 익히는 것을 넘어, 세상을 더 객관적으로 바라보는 눈을 갖는 과정입니다. 그중에서도 오늘 배울 독립표본 t검정(Independent Samples t-Test)은 통계학의 수많은 분석 도구 중에서도 매우 실용적이며, 실제 연구나 비즈니스 분석, 심지어 언론 보도나 정책 판단에서도 빈번하게 활용되는 중요한 기법입니다.

왜냐하면, 우리는 현실에서 무언가를 비교하고 싶어 할 때가 많기 때문입니다. 예를 들어,

“남성과 여성의 하루 평균 스마트폰 사용 시간이 다를까?”
“코로나 이후 재택근무자와 출근근무자의 업무 만족도에 차이가 있을까?”
“A반과 B반의 수학 시험 성적은 차이가 있는가?”
“신제품을 사용한 집단과 기존 제품을 사용한 집단 사이에 구매 만족도의 차이가 있는가?”

이러한 질문은 모두 두 개의 독립된 집단 사이의 평균 차이를 알아보고자 할 때 발생합니다. 이때 사용하는 분석 도구가 바로 오늘의 주제인 독립표본 t검정입니다.

t검정은 그룹 간의 차이를 수치나 평균값 비교로 보는 것이 아니라, 그 차이가 ‘우연에 의한 것인지’ 아니면 ‘실제로 의미 있는 것인지’를 검정하는 통계적 방법입니다. 즉, 겉보기에 평균이 다르더라도 그것이 통계적으로 유의한 차이인지 아닌지를 p값(p-value)이라는 중요한 수치를 통해 판단할 수 있게 해주는 것이지요.

t검정은 특히 심리학, 교육학, 사회과학, 경영학, 의학 연구 등에서 매우 자주 사용되며, 실험군과 통제군의 효과 비교에서도 기본이 되는 도구입니다. 예컨대 어떤 신약이 기존 약보다 효과가 좋은지를 확인하거나, 특정 교육 프로그램이 실제로 학생들의 성적 향상에 도움이 되는지를 검증할 때도 독립표본 t검정이 사용됩니다.

하지만 많은 사람들이 통계 초보 단계에서 t검정을 어려워하는 이유는 다음과 같은 배경 개념들이 함께 따라오기 때문입니다:

등분산성(Variance Homogeneity): 두 집단의 분산이 같다는 가정
정규성(Normality): 데이터가 정규분포를 따른다는 전제
샘플의 독립성(Independence): 각 집단이 서로 독립적인 데이터임을 전제로 함

이러한 개념들은 t검정이 평균 계산이 아니라 가설검정의 구조와 논리에 따라 엄격한 기준 아래 해석되어야 한다는 점을 알려줍니다.

오늘 우리는 이 복잡한 듯 보이는 독립표본 t검정을 아주 쉽게, 단계별로 풀어가며 배워볼 것입니다. 특히, Jamovi라는 무료 통계 분석 소프트웨어를 활용하여 실제 데이터에 t검정을 적용하는 실습을 병행하면서 이론과 실전을 동시에 익히는 구조로 학습하겠습니다.

Jamovi는 마우스 클릭만으로도 평균, 표준편차, t값, p값, 등분산 여부 등을 손쉽게 확인할 수 있도록 해주며, 전문가 수준의 분석 결과를 초보자도 무리 없이 해석할 수 있게 도와주는 도구입니다.

앞으로 다룰 내용은 다음과 같습니다:

독립표본 t검정의 개념과 원리
t값과 p값의 의미
등분산성 검정 (Levene’s Test)
Jamovi에서 t검정 수행 절차
결과 해석과 실제 적용 사례

이번 학습을 통해 여러분은 두 집단 간 평균 차이가 추정이 아닌 통계적으로 검증된 결론임을 어떻게 판단하고 해석하는지에 대해 명확히 이해하게 될 것입니다. 나아가 여러분이 논문을 쓰거나, 연구 데이터를 해석하거나, 사업 보고서를 작성할 때 매우 유용한 역량이 되어줄 것입니다.

1. 독립표본 t검정이란?

독립표본 t검정(Independent Samples t-Test)은 두 개의 서로 다른 집단이 특정 변수에 대해 평균적으로 유의미한 차이가 있는지를 통계적으로 검정하는 방법입니다. 이때 "독립표본"이라는 말은 두 집단의 구성원이 겹치지 않고 독립적이라는 뜻입니다.

✔ 예시:

남성과 여성의 시험 점수가 다른가?
실험군과 통제군의 제품 만족도가 다른가?
수도권과 비수도권 학생의 스트레스 수준이 다른가?

이런 질문은 평균 차이로만 판단할 수 없습니다. 집단 간의 평균이 달라도 통계적으로 유의한 차이인지, 아니면 우연히 생긴 차이인지를 검정해야 합니다. 바로 그 역할을 하는 것이 독립표본 t검정입니다.

2. 검정의 수학적 기초 – t값은 어떻게 계산되나?

독립표본 t검정은 다음 공식을 기반으로 계산됩니다:

$$
t = \frac{\bar{X}_1 - \bar{X}_2}{\sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}}
$$

여기서:

$\bar{X}_1, \bar{X}_2$: 각 집단의 평균
$s_1^2, s_2^2$: 각 집단의 분산
$n_1, n_2$: 각 집단의 표본 수

분모는 두 집단의 분산을 표본 크기만큼 나눈 값들의 합으로 구성되며, 분자가 크고 분모가 작을수록 두 평균 차이가 유의미하다는 것을 의미합니다.

이 t값을 통해 t-분포표에 근거한 p값(p-value)을 산출하고, 일반적으로 p < 0.05일 때 통계적으로 유의한 차이라고 해석합니다.

3. 독립표본 t검정의 전제 조건

정확한 검정을 위해 다음과 같은 전제 조건이 충족되어야 합니다:

조건 항목	내용	검정 방법
독립성	두 집단은 서로 독립적인 데이터여야 함	실험 설계 시 주의
정규성	각 집단의 데이터가 정규분포를 따른다고 가정	샤피로-윌크 검정(Shapiro-Wilk Test), 히스토그램
등분산성	두 집단의 분산이 같다고 가정	Levene’s Test (르빈 검정)

만약 정규성이나 등분산성이 충족되지 않는다면,

비모수 검정 (Mann-Whitney U test)
Welch t-test (등분산 가정 불필요한 버전)을 사용할 수 있습니다.

4. Jamovi에서 독립표본 t검정 실습하기

준비: Jamovi에서 데이터 파일 불러오기

.csv, .xlsx, .sav 등의 파일을 열 수 있습니다.
예시 데이터:
- group: 집단 변수 (예: 남성, 여성)
- score: 연속형 변수 (예: 시험 점수)

실습예제 다운로드

분석 절차

Jamovi 실행 → 상단 메뉴에서 Analyses 클릭
T-Tests → Independent Samples T-Test 선택
Dependent Variables에 비교할 연속형 변수 입력 (score)
Grouping Variable에 집단 구분 변수 입력 (group)
Assumption Checks에서 다음 항목 체크:
- Equality of variances test (Levene’s Test)
- Normality test
- Descriptive statistics
- Effect size (Cohen’s d)
Results 출력 확인

📊 결과 해석 예시

Group	Mean	SD	N
남성	75.3	8.2	30
여성	69.1	9.5	30

Test	t	df	p
Equal variances assumed	2.96	58	0.0047

p = 0.0047 < 0.05 → 통계적으로 유의한 차이
Cohen’s d = 0.65 → 중간 정도의 효과크기 (0.5 ~ 0.8: 중간)

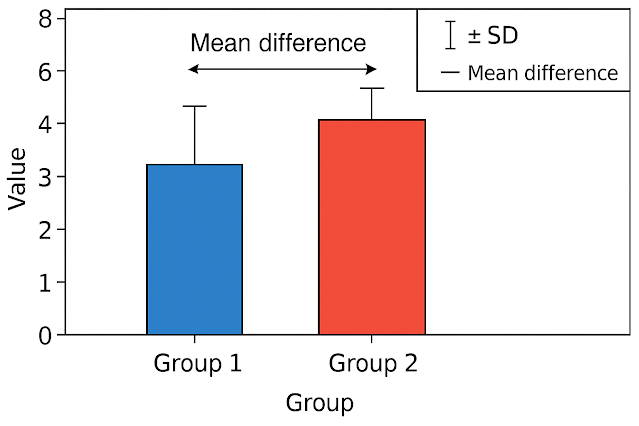
5. Levene’s Test: 등분산 가정 확인

Levene’s Test 결과 p > 0.05이면 등분산 가정이 충족됩니다.
반대로 p < 0.05이면 분산이 다르다는 뜻이므로, Welch’s t-test 결과를 보고 해석합니다.

Jamovi에서는 이 모든 계산을 자동으로 처리해주며, 각 결과 테이블에 해석에 필요한 정보를 함께 표시해줍니다.

6. 실생활 적용 사례

분야	비교 내용	분석 목적
교육	온라인 수업 vs 오프라인 수업의 시험 성적	교육 방식 효과 검증
심리	치료 전 vs 치료 후 불안 점수 비교	심리 치료 효과 확인
마케팅	광고 시청 그룹 vs 비시청 그룹의 브랜드 인지도	광고 효과 측정
의료	신약 투여 그룹 vs 일반약 투여 그룹의 회복 시간	신약 효과 검증

이러한 분석은 ‘차이 비교’가 아니라 실제로 그 차이가 의미 있는가?를 판단하는 데에 매우 중요한 역할을 합니다.

7. Jamovi 실습 예제: 두 집단의 시험 점수 비교

ID	Group	Score
1	A반	78
2	A반	82
3	A반	85
…	…	…
11	B반	72
12	B반	75
13	B반	69

Jamovi에서 Group을 그룹변수로, Score를 종속변수로 지정하면, 평균, 표준편차, t값, p값, 효과크기까지 한 번에 확인할 수 있습니다.

8. 효과크기(Cohen’s d)의 해석

효과크기는 실제로 얼마나 큰 차이인지를 보여줍니다.

Cohen’s d	해석
0.2 이하	매우 작은 차이
0.2 ~ 0.5	작은 차이
0.5 ~ 0.8	중간 차이
0.8 이상	큰 차이

이 지표는 p값과 함께 반드시 해석해야 하는 지표이며, 차이가 유의하더라도 의미가 있는 차이인지를 판단하는 데 매우 중요합니다.

두 집단의 차이를 수치로 말하다 – 독립표본 t검정으로 얻는 통계적 통찰

“차이가 있다고 말할 수 있는가?”라는 질문은 일상에서 매우 자주 접하게 됩니다. 마케팅 분석에서 고객 반응을 비교할 때, 교육 평가에서 수업 방식의 효과를 검증할 때, 심리학 실험에서 치료 전후 변화를 관찰할 때, 우리는 ‘차이’를 확인하고 싶어 합니다. 그리고 그 차이를 근거 있게, 과학적으로, 설득력 있게 설명할 수 있어야 합니다. 바로 그 순간 필요한 것이 독립표본 t검정입니다.

오늘 배운 독립표본 t검정은 두 평균의 차이가 아닌, 그 차이가 통계적으로 유의미한지를 판단하는 절차였습니다. 다시말해, "보이는 차이"가 아닌 "의미 있는 차이"를 찾아내는 과정이며, 통계적 사고의 핵심이라 할 수 있습니다.

이제 우리는 t값이 집단 간의 차이가 우연히 발생했을 확률을 보여주는 지표라는 것을 알게 되었습니다. 특히 p값(p-value)은 이 검정의 핵심입니다. p < 0.05이면 통계적으로 유의하다고 판단하며, 우리가 연구 또는 실험 결과를 발표할 때 강력한 증거가 됩니다.

하지만 여기서 멈추어서는 안 됩니다. 효과크기(Cohen’s d)의 해석 역시 함께 고려해야 합니다. 왜냐하면, 어떤 차이가 p값 기준으로 유의미하더라도 실제로는 ‘무의미하게 작은 차이’일 수 있기 때문입니다. 그래서 우리는 “차이는 있는가?”라는 질문뿐 아니라 “그 차이가 실제로 중요한가?”라는 질문에도 답해야 하는 것입니다.

Jamovi를 활용한 분석 실습은 이러한 이론을 매우 직관적으로 체득할 수 있게 도와주었습니다. 데이터 입력, 변수 지정, 분석 설정, 결과 출력까지 몇 번의 클릭으로 진행되며, 정규성 검정, 등분산 검정(Levene’s Test), t값, p값, 평균차, 표준편차, 효과크기 등 모든 결과가 보기 좋게 제시됩니다. 초보자도 손쉽게 전문적인 분석을 수행할 수 있는 도구로서 Jamovi는 통계 학습의 훌륭한 동반자입니다.

또한, 오늘 배운 내용은 숫자에 숨어 있는 집단 간 차이의 구조를 읽고, 이를 근거로 정책이나 전략을 제안할 수 있는 능력은 모든 분야에서 매우 중요합니다. 특히 사회과학, 교육, 경영, 의학, 공공정책 분야의 연구자에게는 필수적인 역량입니다.

이제 여러분은 다음과 같은 질문에 자신 있게 답할 수 있어야 합니다.

“이 두 집단의 차이는 우연일까, 실제일까?”
“p값과 효과크기를 함께 봐야 하는 이유는 무엇인가?”
“등분산성이란 무엇이며, Levene’s Test는 왜 필요한가?”
“Jamovi에서 어떤 옵션을 체크해야 정확한 분석이 가능한가?”

🌱 다음 학습 안내

Day 14에서는 더 복잡한 비교 분석 기법인 일원분산분석(ANOVA)에 대해 학습할 예정입니다. t검정이 두 집단의 비교라면, ANOVA는 세 집단 이상의 평균을 비교할 수 있게 해줍니다. 그리고 Post-hoc 검정(Bonferroni, Tukey)과 함께, 집단 간 구체적인 차이를 파악하는 더 정교한 분석법을 배울 수 있습니다.

저작자표시 비영리 변경금지 (새창열림)